題目 1713:
數(shù)據(jù)結(jié)構(gòu)-平衡二叉樹的基本操作
時(shí)間限制: 2s
內(nèi)存限制: 96MB 提交: 139 解決: 89
題目描述
平衡二叉樹又稱AVL樹,它是一種具有平衡因子的特殊二叉排序樹。平衡二叉樹或者是一棵空樹,或者是具有以下幾條性質(zhì)的二叉樹:
1. 若它的左子樹不空,則左子樹上所有結(jié)點(diǎn)的值均小于它的根節(jié)點(diǎn)的值;
2. 若它的右子樹不空,則右子樹上所有結(jié)點(diǎn)的值均大于它的根節(jié)點(diǎn)的值;
3. 它的左右子樹也分別為平衡二叉樹,且左子樹和右子樹的深度之差的絕對(duì)值不超過1。
若將二叉樹上結(jié)點(diǎn)的平衡因子定義為該結(jié)點(diǎn)的左子樹深度減去它的右子樹的深度,則平衡二叉樹上的所有結(jié)點(diǎn)的平衡因子只可能為-1、0和1。只要二叉樹上有一個(gè)結(jié)點(diǎn)的平衡因子的絕對(duì)值大于1,則這棵二叉樹就是不平衡的。
通過平衡二叉樹的性質(zhì)不難得知,其插入、刪除、查詢都操作的時(shí)間復(fù)雜度均為O(log2n)。
維持平衡二叉樹性質(zhì)的操作可以被稱為旋轉(zhuǎn)。其中平衡二叉樹的右旋處理可以描述如下:
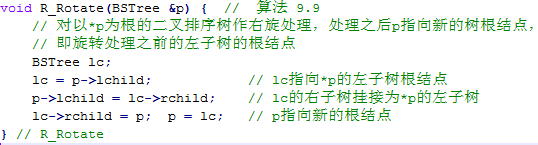
而其左旋處理與右旋正好相反,可以描述如下:
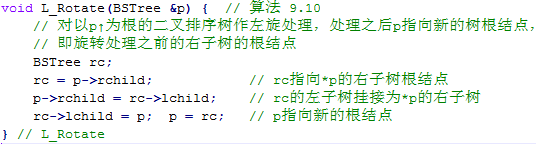
在本題中,讀入一串整數(shù),首先利用這些整數(shù)構(gòu)造一棵平衡二叉樹。另外給定多次查詢,利用構(gòu)造出的平衡二叉樹,判斷每一次查詢是否成功。
輸入格式
輸入的第一行包含2個(gè)正整數(shù)n和k,分別表示共有n個(gè)整數(shù)和k次查詢。其中n不超過500,k同樣不超過500。
第二行包含n個(gè)用空格隔開的正整數(shù),表示n個(gè)整數(shù)。
第三行包含k個(gè)用空格隔開的正整數(shù),表示k次查詢的目標(biāo)。
輸出格式
只有1行,包含k個(gè)整數(shù),分別表示每一次的查詢結(jié)果。如果在查詢中找到了對(duì)應(yīng)的整數(shù),則輸出1,否則輸出0。
請(qǐng)?jiān)诿總€(gè)整數(shù)后輸出一個(gè)空格,并請(qǐng)注意行尾輸出換行。
樣例輸入
8 3 1 3 5 7 8 9 10 15 9 2 5
樣例輸出
1 0 1
提示
零基礎(chǔ)同學(xué)可以先學(xué)習(xí)視頻課程,包含C/C++、Python、百練、藍(lán)橋杯輔導(dǎo)、算法數(shù)據(jù)結(jié)構(gòu)等課程,提供視頻講解以及配套習(xí)題,還有老師答疑,點(diǎn)擊這里了解課程詳情