在對無向圖進(jìn)行遍歷時，對于連通圖，僅需從圖中任一頂點出發(fā)，進(jìn)行深度優(yōu)先搜索或廣度優(yōu)先搜索，便可訪問到圖中所有頂點。對于非連通圖，則需從多個頂點出發(fā)進(jìn)行搜索，而每一次從一個新的起始點出發(fā)進(jìn)行搜索的過程中得到的頂點訪問序列恰為其各個連通分量中的頂點集。

對于非連通圖，每個連通分量中的頂點集，和遍歷時走過的邊一起構(gòu)成若干棵生成樹，這些連通分量的生成樹組成非連通圖的生成森林。

假設(shè)以孩子兄弟鏈表作為生成森林的存儲結(jié)構(gòu)，則生成非連通圖的深度優(yōu)先生成森林的算法可以描述如下：

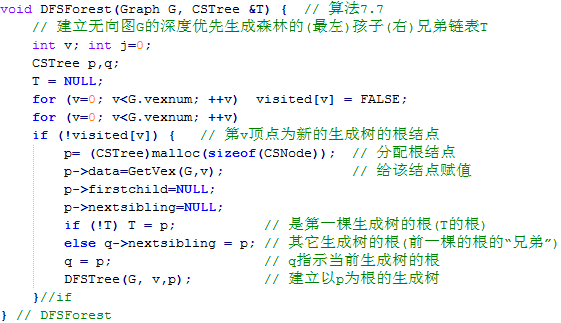
而建立以p為根的深度優(yōu)先生成樹的算法可以描述如下：

在本題中，讀入一個無向圖的鄰接矩陣（即數(shù)組表示），建立無向圖并按照以上描述中的算法建立無向圖的生成森林。對于森林中的每一棵生成樹，遍歷所有頂點，并輸出遍歷頂點的順序。

輸入的第一行包含一個正整數(shù)n，表示圖中共有n個頂點。其中n不超過50。

以后的n行中每行有n個用空格隔開的整數(shù)0或1，對于第i行的第j個0或1，1表示第i個頂點和第j個頂點有直接連接，0表示沒有直接連接。當(dāng)i和j相等的時候，保證對應(yīng)的整數(shù)為0。

輸入保證鄰接矩陣為對稱矩陣，即輸入的圖一定是無向圖。

每一行輸出無向圖中的一棵生成樹，表示按照題目描述中的深度優(yōu)先遍歷算法遍歷相應(yīng)的連通分量的訪問頂點順序。每個整數(shù)后輸出一個空格，并請注意行尾輸出換行。